(·湖州市 第22题 10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
已知抛物线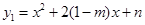 经过点(
经过点(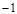 ,
,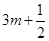 ).
).
(1)求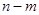 的值;
的值;
(2)若此抛物线的顶点为(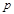 ,
,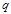 ),用含
),用含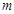 的式子分别表示
的式子分别表示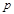 和
和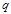 ,并求
,并求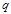 与
与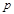 之间的函数关系式;
之间的函数关系式;
(3)若一次函数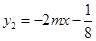 ,且对于任意的实数
,且对于任意的实数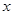 ,都有
,都有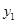 ≥
≥ ,直接写出
,直接写出 的取值范围.
的取值范围.
阅读下面的材料:
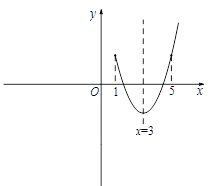
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数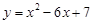 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,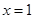 和
和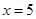 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对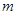 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数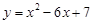 的对称轴为直线
的对称轴为直线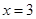 ,
,
∴由对称性可知,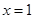 和
和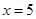 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则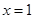 时,
时,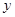 的最大值为2;
的最大值为2;
若m≥5,则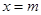 时,
时,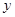 的最大值为
的最大值为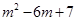 .
.
请你参考小明的思路,解答下列问题:
(1)当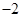 ≤x≤4时,二次函数
≤x≤4时,二次函数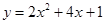 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数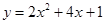 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数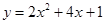 的最大值为31,则
的最大值为31,则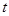 的值为_______.
的值为_______.
平面直角坐标系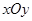 中,原点O是正三角形ABC外接圆的圆心,点A在
中,原点O是正三角形ABC外接圆的圆心,点A在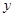 轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△
轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△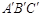 ,点
,点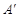 、
、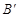 、
、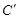 分别为点A、B、C的对应点.
分别为点A、B、C的对应点.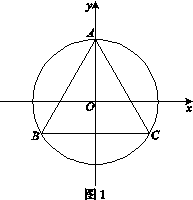

(1)当=60时,
①请在图1中画出△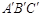 ;
;
②若AB分别与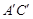 、
、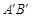 交于点D、E,则DE的长为_______;
交于点D、E,则DE的长为_______;
(2)如图2,当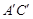 ⊥AB时,
⊥AB时,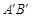 分别与AB、BC交于点F、G,则点
分别与AB、BC交于点F、G,则点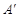 的坐标为 _____,△FBG的周长为_____,△ABC与△
的坐标为 _____,△FBG的周长为_____,△ABC与△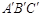 重叠部分的面积为_______.
重叠部分的面积为_______.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.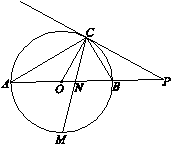
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若MN MC=8,求⊙O的直径.
已知抛物线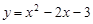 .
.
(1)它与x轴的交点的坐标为_______;
(2)在坐标系中利用描点法画出它的图象;
(3)将该抛物线在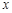 轴下方的部分(不包含与
轴下方的部分(不包含与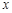 轴的交点)记为G,若直线
轴的交点)记为G,若直线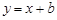 与G 只有一个公共点,则
与G 只有一个公共点,则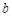 的取值范围是_______.
的取值范围是_______.