如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.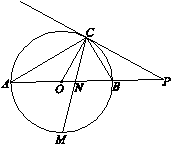
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若MN MC=8,求⊙O的直径.
为增加学生阅读量,某校购买了“科普类”和“文学类”两种书籍,购买“科普类”图书花费了3600元,购买“文学类”图书花费了2700元,其中“科普类”图书的单价比“文学类”图书的单价多 ,购买“科普类”图书的数量比“文学类”图书的数量多20本.
(1)求这两种图书的单价分别是多少元?
(2)学校决定再次购买这两种图书共100本,且总费用不超过1600元,求最多能购买“科普类”图书多少本?
李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有: .转移注意力, .合理宣泄, .自我暗示, .放松训练.
(1)若小如随机取走一个锦囊,则取走的是写有“自我暗示”的概率是 ;
(2)若小如和小意每人先后随机抽取一个锦囊(取走后不放回),请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的概率.
为加强交通安全教育,某中学对全体学生进行“交通知识”测试,学校随机抽取了部分学生的测试成绩,并根据测试成绩绘制两种统计图表(不完整),请结合图中信息解答下列问题:
学生测试成绩频数分布表
|
组别 |
成绩 分 |
人数 |
|
|
|
8 |
|
|
|
|
|
|
|
24 |
|
|
|
|
(1)表中的 值为 , 值为 ;
(2)求扇形统计图中 部分所在扇形的圆心角度数;
(3)若测试成绩80分以上(含80分)为优秀,根据调查结果请估计全校2000名学生中测试成绩为优秀的人数.

先化简,再求值: ,其中 .
如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,连接 , ,点 是抛物线第一象限上的一动点,过点 作 轴于点 ,交 于点 .
(1)求抛物线的解析式;
(2)如图1,作 于点 ,使 ,以 , 为邻边作矩形 .当矩形 的面积是 面积的3倍时,求点 的坐标;
(3)如图2,当点 运动到抛物线的顶点时,点 在直线 上,若以点 、 、 为顶点的三角形是锐角三角形,请直接写出点 纵坐标 的取值范围.
