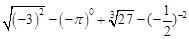(·湖北孝感)已知关于x的一元二次方程:
(1)试判断原方程根的情况;
(2)若抛物线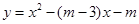 与
与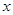 轴交于
轴交于 两点,则
两点,则 ,
, 两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:
两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示: )
)
图1,两个不全等的等腰直角三角形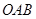 和
和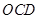 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点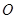 .
.
⑴在图1中,你发现线段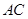 ,
,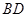 的数量关系是,直线
的数量关系是,直线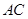 ,
,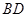 相交成度角.
相交成度角.
⑵将图1中的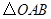 绕点
绕点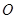 顺时针旋转
顺时针旋转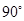 角,得到图2,这时(1)中的两个结论是否成立?请做出判断并说明理由.
角,得到图2,这时(1)中的两个结论是否成立?请做出判断并说明理由.
⑶将图1中的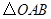 绕点
绕点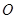 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?(请直接回答结论)
顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?(请直接回答结论)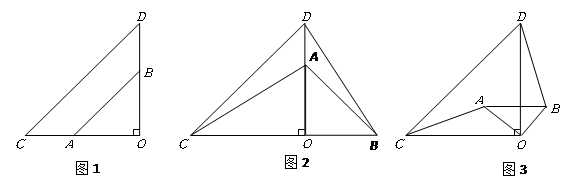
如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=CD.E、F分别在AD、CD上,DE=CF,AF、BE交于点P.
⑴试说明:AF=BE⑵猜测∠BPF的度数,并说明你的结论的正确性.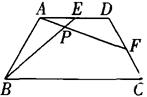
如图,在一棵树的10 高B处有2只猴子,一只猴子爬到树下走到离树20
高B处有2只猴子,一只猴子爬到树下走到离树20 处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.
处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.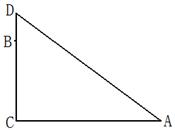
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=4m, AD=3m,CD=2m,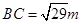 ,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?
,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?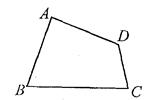
计算: