（·湖南常德）某物流公 司承接A、B两种货物运输业务，已知5月份A货物运费单价为50元/吨，B货物运费单价为30元/吨，共收取运费9500元；6月份由于油价上涨，运费单价上涨为：A货物70元/吨，B货物40元/吨；该物流公司6月承接的A种货物和B种数量与5月份相同，6月份共收取运费13000元。
（1）该物流公司月运输两种货物各多少吨？
（2）该物流公司预计7月份运输这两种货物330吨，且A货物的数量不大于B货物的2倍，在运费单价与6月份相同的情况下，该物流公司7月份最多将收到多少运输费？
如图，甲、乙两人分别从A（1，
）、B（6，0）两点同时出发，点O为坐标原点，甲沿AO方向，乙沿BO方向均以4km／h的速度行走．th后，甲到达M点，乙到达N点．
（1）请说明甲、乙两人到达O点前，MN与AB不可能平行；
（2）当t为何值时，△OMN∽△OBA？
如图，A（1，0），B（3，0），C（0，3），D（2，－1），P（2，2）．
（1）问：△ABC与△ADP相似吗？说明理由；
（2）在图中标出点D关于y轴的对称点D′，连接AD′、CD′，判断△ACD′的形状，并说明理由；
（3）求∠OCA＋∠OCD的度数．
如图所示，有一张矩形纸片ABCD，E、F分别是BC、AD上的点（不与顶点重合）．如果直线EF将矩形分成面积相等的两部分，那么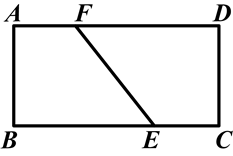
（1）得到的两个四边形是否相似？若相似，请求出相似比；若不相似，请说明理由；
（2）这样的直线可以作多少条？
如图，各组中的两个图形，哪些是相似的图形，哪些不是？
如图，在边长为2的正方形ABCD中，G是AD延长线上的一点，且DG=AD，动点M从A出发，以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动（M不与A、G重合），设运动时间为t秒。连接BM并延长交AG于N。
（1）是否存在点M，使△ABM为等腰三角形？若存在，分析点M的位置；若不存在，请说明理由；
（2）当点N在AD边上时，若BN⊥HN，NH交∠CDG的平分线于H，求证：BN=NH；
（3）过点M分别用AB、AD的垂线，垂足分别为E、F，矩形AEMF与△ACG重叠部分的面积为S，求S的最大值。