已知关于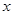 的方程
的方程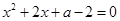 .
.
(1)若该方程有两个不相等的实数根,求实数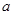 的取值范围;
的取值范围;
(2)若该方程的一个根为1,求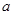 的值及该方程的另一根.
的值及该方程的另一根.
(本题满分10分)
已知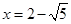 ,
,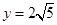 ,求
,求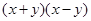 的值.
的值.
如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段AC于点M,K.
(1)观察:①如图2、图3,当∠CDF=0°或60°时,AM+CK______MK(填“>”,“<”或“=”);
②如图4,当∠CDF=30°时,AM+CK______MK(只填“>”或“<”);(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK______MK(填“>”,“<”或“=”),并说明理由;
(3)如果MK2+CK2=AM2,请直接写出∠CDF的度数和
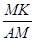 的值.
的值.
光明中学计划从荣威公司购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据光明中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的
 .请你通过计算,求出光明中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
.请你通过计算,求出光明中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
长方形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,并使它的一条直角边过A点,另一条直角边交CD于E点.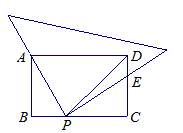
(1)找出图中与PA相等的线段.并说明理由.
(2)若点E为CD的三等分点,且BC=6,求BP的长.
光明中学数学活动小组为了调查居民的用水情况,从某社区的500户家庭中随机抽取了20户家庭的月用水量,结果如下表所示:
| 月用水量(吨) |
10 |
15 |
20 |
25 |
| 户数 |
8 |
6 |
4 |
2 |
(1)求这20户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量.