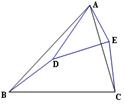
已知:如图, 为锐角三角形, .

求作:线段 BP ,使得点 P 在直线 CD 上,且 .
作法:①以点 A 为圆心, AC 长为半径画圆,交直线 CD 于 C , P 两点;②连接 BP .线段 BP 就是所求作线段.
( 1 )使用直尺和圆规,依作法补全图形(保留作图痕迹)
( 2 )完成下面的证明.
证明: ,
.
,
∴点 B 在⊙ A 上.
又∵ ( )(填推理依据)
∴
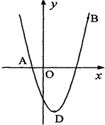
如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请
解答下列问题:求抛物线的解析式;
若抛物线的顶点为点D,对称轴所在的直线交x轴于点E,连接AD,点F为AD的中点,求出线段EF的长。
注:抛物线y=ax2+bx+c的对称轴是x=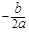 ,顶点坐标是(
,顶点坐标是(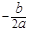 ,
,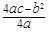 )。
)。
如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、
(-1,0)、(1,0)、(-1,-1)。求经过A、B、C三点的抛物线的表达式;
以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。

深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信
息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。求该宾馆共有多少间住房,每间住房每天收费多少元?
通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。写出图中两对相似三角形(不得添加辅助线);
请分别说明两对三角形相似的理由。
已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图示)。当n=8时,共向外做出了18个
小等边三角形;当n=k时,共向外做出了3(k-2)个小等边三角形,这些小等边角形的面积和是3(k-2)k2S(用含k的式子表示)。