如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=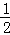 x刻画.
x刻画.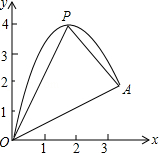
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
如图,已知抛物线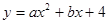 与
与 轴交于
轴交于 (
( ,0)、
,0)、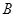 两点,与
两点,与 轴交于
轴交于 点,其对称轴为直线
点,其对称轴为直线 .
.
(1)求抛物线的解析式;
(2)把线段 沿
沿 轴向右平移,设平移后
轴向右平移,设平移后 、
、 的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由。
端午节期间,某食品店平均每天可卖出300只粽子,且卖出1只粽子的利润是1元。经调查发现,零售单价每降0.1元,每天可多卖出100只粽子。为了使每天获取的利润更多,该店决定把零售单价下降 元。在不考虑其他因素的条件下,当
元。在不考虑其他因素的条件下,当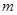 定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),
(1)试确定此二次函数的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使PB+PC的值最小,如果存在,请求出点P的坐标,如果不存在,请说明理由。
六一儿童节,某学习用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。其中,书包每个定价20元,水性笔每支定价5元。小丽和同学需买4个书包,水性笔若干支(不少于4支)。
(1)分别写出两种优惠方法购买费用 (元)与所买水性笔支数
(元)与所买水性笔支数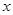 (支)的函数解析式(请化简函数解析式);
(支)的函数解析式(请化简函数解析式);
(2)对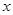 的取值情况进行分析,说明按哪种优惠方法购买比较便宜。
的取值情况进行分析,说明按哪种优惠方法购买比较便宜。
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线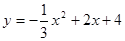 的一部分。
的一部分。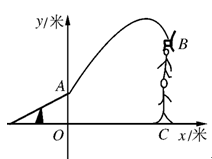
(1)求演员弹跳离地面的最大高度;
(2)已知在一次表演中,人梯高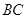 =4米,人梯到起跳点
=4米,人梯到起跳点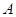 的水平距离是6米,问这次表演是否成功?请说明理由。
的水平距离是6米,问这次表演是否成功?请说明理由。