如图,在平行四边形ABCD中,AB<BC.
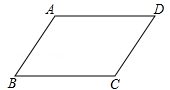
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D已知经过点D的⊙O切线恰好经过点C
(1)试判断CD与AC的位置关系,并证明;
(2)若△ACB∽△CDB,且AC=3,求图中阴影部分的面积
如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米.参考数据:sin32°=0.5299,cos32°=0.8480)
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.
(1)求A、B两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当y >y
>y 时x的取值范围;
时x的取值范围;
(3)求△AOB的面积.
如图1,△ABC中,BC=25,BC边上的高为20,将AB,AC分别n等分,连接两边对应的等分点,以这些连接线为一边做矩形,使这些矩形的边B1C1,B2C2,B3C3……的对应边分别为 B2C2,B3C3,B4C4……
(1)若n=5,如图2,求B3C3为一边的矩形的面积;
(2)若n=5,求所有矩形的面积和;
(3)当分为n等分时,你能用含有n的表达式表示所有矩形的面积和吗?
如图,一次函数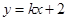 的图象与反比例函数
的图象与反比例函数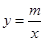 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交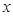 轴、
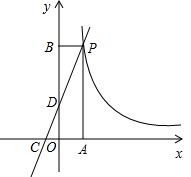
轴、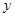 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当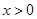 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的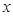 的取值范围.
的取值范围.