定义:长宽比为
：1（n为正基数）的矩形称为株为矩形．下面，我们通过折叠的方式折出一个
矩形．如图①所示．
操作1：将正方形ABCD沿过点B的直线折叠，使折叠后的点C落在对角线BD上的点G处，折痕为BH
操作2：将AD沿过点G的直线折叠，使点A，点D分别落在边AB，CD上，折痕为EF
则四边形BCEF为矩形
证明：设正方形ABCD的边长为1，则BD=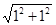
=．
由折叠性质可知BG=BC=1，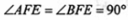
，则四边形BCEF为矩形
阅读以上内容，回答下列问题：
在图①中，所有与CH相等的线段是 ，tan
的值是
已知四边形BCEF为矩形，模仿上述操作，得到四边形BCMN，如图
。
求证：四边形BCMN是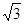
矩形
将图②中的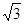矩形BCMN沿用（2）中的操作3次后，得到一个“矩形”，则n的值是
某班到毕业时共结余经费1800元，班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品，其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念．已知每件文化衫比每本相册费9元，用200元恰好可以买到2件文件衫和5本相册．
（1）求每件文化衫和每本相册的价格分别为多少元？
（2）有几种购买文化衫和相册的方案？哪种方案用于购买老师纪念品的资金更充足？
某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本
和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．
（1）请写出y关于x的关系式；
（2）如果该厂每天至少投入成本30000元，那么每天至少获利多少元？
（3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？
| A |
B |
|
| 成本（元） |
50 |
35 |
| 利润（元） |
20 |
15 |
九年级六班的一个综合实践活动小组去A，B两超市调查去年和今年“十一”期间的销售情况，如图是调查后小敏与其他两位同学进行交流的情景．根据他们的对话，请你分别求出A，B两个超市今年“十一”期间的销售额．
小明画了如下的一张表格，并在表格中圈出了一个竖列上相邻的三个数，他把这三个数的和告诉了同伴，要同伴求出这三个数．
（1）当这三个数的和是138时，能否求出这三个数？请你也试一试；
| 1 |
4 |
7 |
10 |
13 |
16 |
| 19 |
22 |
25 |
28 |
31 |
34 |
| 37 |
40 |
43 |
46 |
49 |
52 |
| 55 |
58 |
61 |
64 |
67 |
70 |
（2）当这三个数的和是148呢？
求不等式组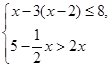
的整数解，并在数轴上表示出来．