如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,池塘边一棵垂直于水面 的笔直大树 在点 处折断, 部分倒下,点 与水面上的点 重合,部分沉入水中后,点 与水中的点 重合, 交水面于点 , , , ,求 部分的高度.(精确到 .参考数据: ,
随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
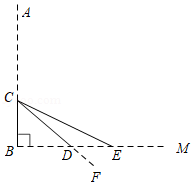
如图1, 绕点 顺时针旋转得 ,射线 交射线 于点 .
(1) 与 的关系是 ;
(2)如图2,当旋转角为 时,点 ,点 与线段 的中点 恰好在同一直线上,延长 至点 ,使 ,连接 .
① 与 的关系是 ,请说明理由;
②如图3,连接 , ,若 , ,求线段 的长度.

如图, 是 的直径,点 和点 是 上的两点,连接 , , ,过点 作射线交 的延长线于点 ,使 .
(1)求证: 是 的切线;
(2)若 ,求阴影部分的面积.

我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量 (千克)与销售单价 (元 符合一次函数关系,如图所示.
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)若在销售过程中每天还要支付其他费用450元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
