如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
(1)判断MN与AC的位置关系;
(2)求点D由点A向点B匀速运动的过程中,线段MN所扫过区域的面积;
(3)若△DMN是等腰三角形,求t的值.
如图,正方形ABCD,点E、F分别为BC、CD边上的点,连接EF,点 M为EF上一点,且使AE平分∠BAM,AF平分∠DAM,证明:∠EAF=45°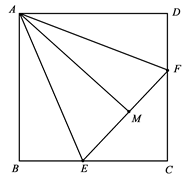
一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)观察表中数据规律填表:
| 餐桌张数 |
1 |
2 |
3 |
4 |
… n |
| 可坐人数 |
6 |
8 |
10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来一起就餐,要拼成一张大餐桌,怎样拼桌需要的餐桌最少?最少要用多少张?
解方程或解不等式组:
(1)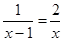 (2)
(2)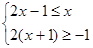
如图:∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为(只添加一个条件即可);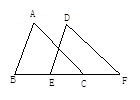
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
.