（柳州）如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数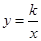
（
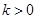）的图象与BC边交于点E．
（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？
有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一
张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．
（1）先后两次抽得的数字分别记为s和t，则︱s－t︱≥1的概率．
（2）甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B
方案：若两次抽得数字和为奇数则甲胜，否则乙胜．
请问甲选择哪种方案胜率更高？
如图，在等腰三角形ABC中，∠ABC＝90°，D为AC边上中点，过D
点作DE⊥DF，交AB于E，交BC于F．若AE＝4，FC＝3，求EF长．
为了加强食品安全管理，有关部门对某大型超市的甲、乙两种品牌食用
油共抽取18瓶进行检测，检测结果分成“优秀”、“合格”、“不合格”三个等级，数据处理
后制成以下折线统计图和扇形统计图．
（1）甲、乙两种品牌食用油各被抽取了多少瓶用于检测？
（2）在该超市购买一瓶乙品牌食用油，请估计能买到“优秀”等级的概率是多少？
如图10所示，Rt△ABC是一张放在平面
直角坐标系中的纸片，点C与原点O重合，点A在x轴的正半轴上，点B在y轴的正半轴上，已知OA=3，OB＝4。将纸片的直角部分翻折，使点C落在AB边上，记为D点，AE为折痕，E在y轴上。
（1）在图10所示的直角坐标系中，求E点的坐标及AE的长。
（2）线段AD上有一动点P（不与A、D重合）自A点沿AD方向以每秒1个单位长度向D点作匀速运动，设运动时间为t秒（0<t<3），过P点作PM∥DE交AE于M点，过点M作MN∥AD交DE于N点，求四边形PMND的面积S与时间t之间的函数关系式，当t取何值时，S有最大值？最大值是多少？
（3）当t（0<t<3）为何值
时，A、D、M三点构成等腰三角形？并求出点M的坐标。