(玉林防城港)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为 的中点,连接DE,EB.
的中点,连接DE,EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为6π,求⊙O的半径r.
已知正方形ABCD,点B与坐标原点O重合,BC、BA分别在x轴和y轴上,对角线BD在射线OM上,点E在y轴上,OA、OE的长分别是2和6,正方形ABCD以每秒2个单位长度的速度沿射线OM(BD始终在射线OM上)方向移动,同时点P从点C以每秒1个单位长度的速度沿折线CD—DA向点A移动,当一点到达终点时,另一点也停止移动,设移动时间为t秒当0≤t≤2时,直接写出点P的坐标(用t的代数式表示).
当四边形EABO是等腰梯形时,①求t的值;②求证:OA=ED
是否存在这样的t值,使EP//x轴,若有,求出点P的坐标;若没有,说明理由。
已知,正方形ABCD,点P在对角线BD上,连接AP、CP(如图①)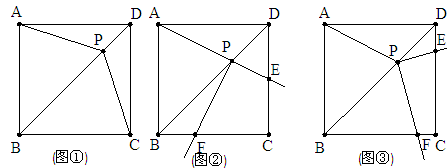
(1)求证:AP=CP.
(2)将一直角三角板的直角顶点置于点P处并绕点P旋转,设两直角边分别交DC、BC于E、F,
a.若旋转到图②位置,使PE与PA在一直线上,求证:PF=PA.
b.若旋转到图③位置且PD∶PB=2∶3,求PE∶PF的值.
如图,已知AB是⊙O的直径,点D、E在⊙O上,且︵AD∶︵DE=3∶5, ︵BE的度数为20°,连接DE并延长交AB的延长线于C,求∠AOD的度数;
判断CE与AB有什么数量关系,并说明理由

我们已经学过用方差来描述一组数据的离散程度,其实我们还可以用“平均差”来描述一组数据的离散程度。在一组数据x1,x2,…,xn中,各数据与它们的平均数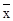 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T= (|x1-
(|x1-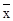 |+|x2-
|+|x2-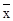 |+…+|xn-
|+…+|xn-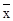 |)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
|)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
请你解决下列问题:分别计算下列甲乙两个样本数据的“平均差”,并根据计算结果判断哪个样本波动较大。
甲:12,13,11,10,14,乙:10,17,10,13,10分别计算甲、乙两个样本数据的方差和标准差,并根据计算结果判断哪个样本波动较大.
以上的两种方法判断的结果是否一致?
某商店9月份的利润是2500元,要使11月的利润达到3600元,平均每月增长的百分率是多少?