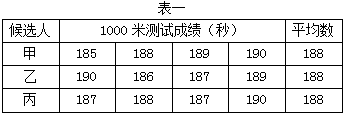
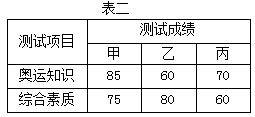
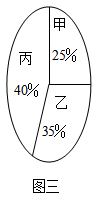
学校要从甲、乙、丙三名中长跑运动员中选出一名奥运火炬传递手.先对三人一学期的1000米测试成绩作了统计分析如表一;又对三人进行了奥运知识和综合素质测试,测试成绩(百分制)如表二;之后在100人中对三人进行了民主推选,要求每人只推选1人,不准弃权,最后统计三人的得票率如图三,一票计2分.
(1)请计算甲、乙、丙三人各自关于奥运知识,综合素质,民主推选三项考查得分的平均成绩,并参考1000米测试成绩的稳定性确定谁最合适.
(2)如果对奥运知识、综合素质、民主推选分别赋予3,4,3的权,请计算每人三项考查的平均成绩,并参考1000米测试的平均成绩确定谁最合适.