如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.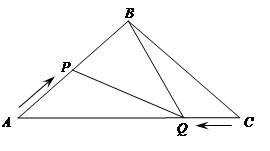
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)当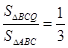 时,求
时,求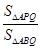 的值.
的值.
计算: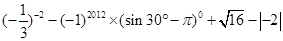 .
.
如图1,将三角板放在正方形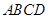 上,使三角板的直角顶点
上,使三角板的直角顶点 与正方形
与正方形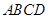 的顶点
的顶点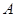 重合,三角扳的一边交
重合,三角扳的一边交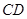 于点
于点 .另一边交
.另一边交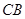 的延长线于点
的延长线于点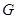 .
.
(1)求证: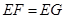 ;
;
(2)如图2,移动三角板,使顶点 始终在正方形
始终在正方形 的对角线
的对角线 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形 ”改为“矩形
”改为“矩形 ”,且使三角板的一边经过点
”,且使三角板的一边经过点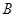 ,其他条件不变,若
,其他条件不变,若 ,求
,求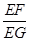 的值.
的值.
某企业决定用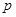 万元援助灾区
万元援助灾区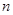 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第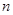 所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中
所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中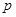 ,
,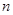 ,
, 都是正整数)
都是正整数)
根据以上信息,解答下列问题:
(1)写出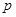 与
与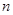 的关系式;
的关系式;
(2)当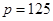 时,该企业能援助多少所学校?
时,该企业能援助多少所学校?
(3)根据震区灾情,该企业计划再次提供不超过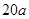 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若 由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
已知一元二次方程 中,如果
中,如果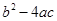 ≥
≥ ,那么它的两个实数根是
,那么它的两个实数根是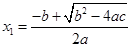 ,
,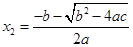 .
.
(1)计算: 、
、 的值(用含
的值(用含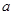 、
、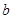 、
、 的代数式表示);
的代数式表示);
(2)设方程 的两个根分别为
的两个根分别为 、
、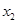 ,根据(1)所求的结果,不解方程,直接写出
,根据(1)所求的结果,不解方程,直接写出 =,
=, =;
=;
(3)如果方程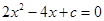 的一根是
的一根是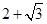 ,请你利用(1)中根与系数的关系求出方程的另一根及
,请你利用(1)中根与系数的关系求出方程的另一根及 的值.
的值.
如图,在矩形中,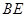 平分
平分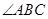 ,交
,交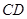 于点
于点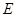 ,点
,点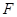 在边
在边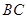 上.
上.
(1)如果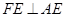 ,那么
,那么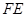 和
和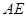 相等吗?证明你的结论.
相等吗?证明你的结论.
(2)如果 ,那么
,那么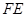 与
与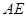 有怎样的位置关系?证明你的结论.
有怎样的位置关系?证明你的结论.