如图1，将三角板放在正方形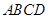
上，使三角板的直角顶点
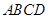与正方形的顶点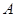
重合，三角扳的一边交
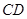于点
．另一边交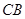
的延长线于点
．
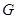（1）求证：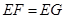
；
（2）如图2，移动三角板，使顶点始终在正方形
的对角线
上，其他条件不变，题（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：
（3）如图3，将（2）中的“正方形”改为“矩形”，且使三角板的一边经过点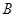
，其他条件不变，若
，求
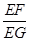的值．
如图，点B和点C分别为∠MAN两边上的点，AB＝AC.
（1）按下列语句画出图形：（要求不写作法，保留作图痕迹）
① AD⊥BC，垂足为D；② ∠BCN的平分线CE与AD的延长线交于点E；③ 连结BE.
（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：
≌，≌；并选择其中的一对全等三角形予以证明.
△ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．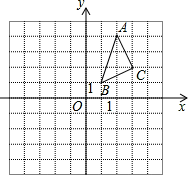
（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．
如图，CE=CB，CD=CA，∠DCA=∠ECB，求证：DE=AB．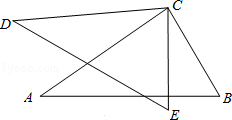
一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是多少？
如图，直线
：
分别与
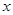轴、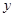
轴交于A、B两点，点C线段AB上，作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE；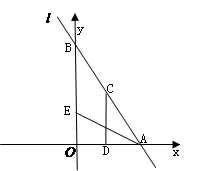
（1）填空：点C的坐标为（，）；点E的坐标为（，）；
（2）直线
过点E，且将△AOB分成面积比为1：2的两部分，求直线的表达式；
（3）点P在x轴上运动，
①当PC+PE取最小值时，求点P的坐标及PC+PE的最小值；
②当PC-PE取最大值时，求点P的坐标及PC-PE的最大值；