已知一元二次方程 中,如果
中,如果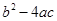 ≥
≥ ,那么它的两个实数根是
,那么它的两个实数根是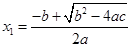 ,
,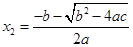 .
.
(1)计算: 、
、 的值(用含
的值(用含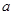 、
、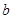 、
、 的代数式表示);
的代数式表示);
(2)设方程 的两个根分别为
的两个根分别为 、
、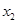 ,根据(1)所求的结果,不解方程,直接写出
,根据(1)所求的结果,不解方程,直接写出 = ,
= , = ;
= ;
(3)如果方程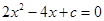 的一根是
的一根是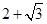 ,请你利用(1)中根与系数的关系求出方程的另一根及
,请你利用(1)中根与系数的关系求出方程的另一根及 的值.
的值.
某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动一次,直到指针指向一个区域内为止),然后,将两次记录的数据相乘.
(1)请利用画树状图或列表的方法,求出乘积为负数的概率;
(2)如果乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
在2014年巴西世界杯足球赛开幕之前,某中学团委为了解本校学生对世界杯足球赛的关注情况,随机调查了部分学生对足球运动的喜欢程度,绘制成如下的两幅不完整的统计图.
请你根据以上统计图提供的信息,回答下列问题:
(1)随机抽查了名学生;
(2)补全图中的条形图;
(3)若全校共有500名学生,请你估计全校大约有多少名学生喜欢(含“较喜欢”和“很喜欢”)足球运动.
先化简,再求值: ,其中x=
,其中x= +1.
+1.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-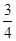 x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。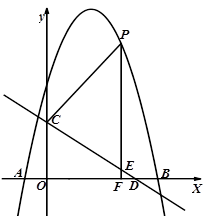
(1)求抛物线的解析式;
(2)若PE =5EF,求m的值;
(3)若点E/是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[50°,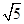 ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.