在2014年巴西世界杯足球赛开幕之前,某中学团委为了解本校学生对世界杯足球赛的关注情况,随机调查了部分学生对足球运动的喜欢程度,绘制成如下的两幅不完整的统计图.
请你根据以上统计图提供的信息,回答下列问题:
(1)随机抽查了 名学生;
(2)补全图中的条形图;
(3)若全校共有500名学生,请你估计全校大约有多少名学生喜欢(含“较喜欢”和“很喜欢”)足球运动.
如图,在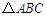 中,AB是⊙O的直径,⊙O与AC交于点D,
中,AB是⊙O的直径,⊙O与AC交于点D,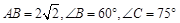 ,求
,求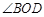 的度数;
的度数;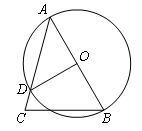
某射击运动员在相同条件下的射击160次,其成绩记录如下:
| 射击次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
| 射中9环以上的次数 |
15 |
33 |
63 |
79 |
97 |
111 |
130 |
|
| 射中9环以上的频率 |
0.75 |
0.83 |
0.80 |
0.79 |
0.79 |
0.79 |
0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.
(1)如图一,图二,等边三角形MNP的边长为1,线段AB的长为4,点M与A重合,点N在线段AB上.△MNP沿线段AB按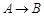 的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为;
的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为;
(2)如图三,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上,点P在正方形内部,正方形MNPQ沿正方形ABCD的边按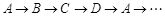 的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为.
的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为.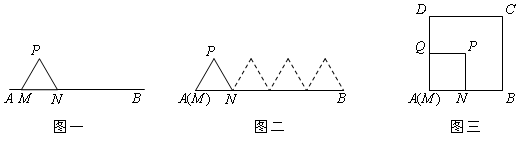
(注:以△MNP为例,△MNP沿线段AB按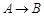 的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时,再以顶点P为中心顺时针旋转,如此继续.多边形沿直线滚动与此类似.)
的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时,再以顶点P为中心顺时针旋转,如此继续.多边形沿直线滚动与此类似.)
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).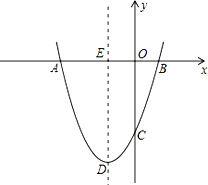
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图所示,E是正方形ABCD的边AB上的动点,正方形的边长为4, EF⊥DE交BC于点F.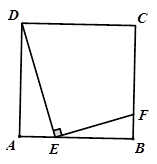

(1)求证:△ADE ∽△BEF ;
(2)AE=x,BF=y.当x取什么值时,y有最大值? 并求出这个最大值;
(3)已知D、C 、F、E四点在同一个圆上,连接CE、DF,若sin∠CEF =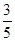 ,求此圆直径.
,求此圆直径.