如图(1),在平面直角坐标系xOy中,抛物线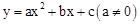 与x轴交于
与x轴交于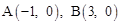 ,与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
,与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是 ;
(2)如图(2),点P是AD上的一个动点, 是P关于DE的对称点,连结PE,过
是P关于DE的对称点,连结PE,过 作
作 F∥PE交x轴于F. 设
F∥PE交x轴于F. 设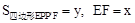 ,求y关于x的函数关系式,并求y的最大值;
,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在,请说明理由.
(本题8分)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400
平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
(本题8分)如图,AB是半圆O的直径,O为AB中点,C、D两点在弧AB上,且AD∥OC,连接BC、BD.若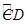 的度数为
的度数为 ,求
,求 的度数.
的度数.
(本题8分)解方程:①
②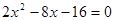 (需用配方法解)
(需用配方法解)
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后
得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.