某企业决定用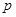
万元援助灾区
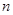所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况，该企业捐款的分配方案如下：所有学校得到的捐款数都相等，到第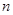所学校的捐款恰好分完，捐款的分配方法如下表所示. (其中,,
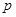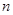都是正整数)
根据以上信息，解答下列问题：
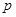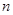(1)写出与的关系式；
(2)当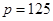
时，该企业能援助多少所学校？
(3)根据震区灾情，该企业计划再次提供不超过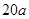
万元的捐款，按照原来的分配方案援助其它学校.若由 (2)确定,则再次提供的捐款最多又可以援助多少所学校？
甲、乙两船分别在相距120米的两平行航线上向东匀速行驶，小明站在甲船的船尾对着乙船拍照，此时他发现乙船的船尾在他们的西偏北30°方向，船头在他的西偏北45°方向．小明迅速用30秒时间走向船头，此时发现乙船船头在他的西偏北60°方向．已知甲船长20米，甲船的速度为600米/分．求乙船的长度和乙船的速度．（结果取整数）（参考数据：
）
如图,已知直线
与坐标轴相交于A、B两点，与双曲线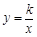
交于点C．A、D两点关于y轴对称若四边形OBCD的面积为6，求k的值．
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E．DF⊥AC于点F．
（1）求证：DF是⊙O的切线．
（2）当∠B的度数是多少时，DE∥AB？并说明理由．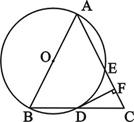
有四部不同的电影，分别记为A, B, C, D．
（1）若甲从中随机选择一部观看，则恰好是电影A的概率是；
（2）若甲从中随机选择一部观看，乙也从中随机选择一部观看，求甲、乙两人选择同一部电影的概率．
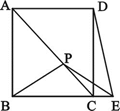
如图，正方形ABCD中,P是AC上一点，E是BC延长线上一点,且PB=PE．若BP=
，求DE的长．