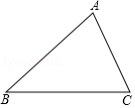
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.DF⊥AC于点F.
(1)求证:DF是⊙O的切线.
(2)当∠B的度数是多少时,DE∥AB?并说明理由.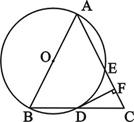
已知 的直径 ,弦 与弦 交于点 .且 ,垂足为点 .

(1)如图1,如果 ,求弦 的长;
(2)如图2,如果 为弦 的中点,求 的余切值;
(3)联结 、 、 ,如果 是 的内接正 边形的一边, 是 的内接正 边形的一边,求 的面积.
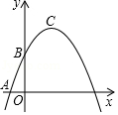
在平面直角坐标系 中(如图).已知抛物线 经过点 和点 ,顶点为 ,点 在其对称轴上且位于点 下方,将线段 绕点 按顺时针方向旋转 ,点 落在抛物线上的点 处.
(1)求这条抛物线的表达式;
(2)求线段 的长;
(3)将抛物线平移,使其顶点 移到原点 的位置,这时点 落在点 的位置,如果点 在 轴上,且以 、 、 、 为顶点的四边形面积为8,求点 的坐标.
已知:如图,正方形 中, 是边 上一点, , ,垂足分别是点 、 .
(1)求证: ;
(2)连接 ,如果 .求证: .

一辆汽车在某次行驶过程中,油箱中的剩余油量 (升 与行驶路程 (千米)之间是一次函数关系,其部分图象如图所示.
(1)求 关于 的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

如图,已知 中, , .
(1)求边 的长;
(2)设边 的垂直平分线与边 的交点为 ,求 的值.