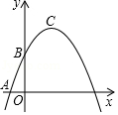
在平面直角坐标系中(如图).已知抛物线经过点和点,顶点为,点在其对称轴上且位于点下方,将线段绕点按顺时针方向旋转,点落在抛物线上的点处.
(1)求这条抛物线的表达式;
(2)求线段的长;
(3)将抛物线平移,使其顶点移到原点的位置,这时点落在点的位置,如果点在轴上,且以、、、为顶点的四边形面积为8,求点的坐标.
(年湖北襄阳10分)如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.
(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
(年浙江宁波14分)木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼接到矩形AEFD下面,并利用拼成的木板锯一个尽可能大的圆.
(1)写出方案一中的圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE= (
( ),圆的半径为
),圆的半径为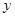 ,
,
①求 关于
关于 的函数解析式;
的函数解析式;
②当 取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?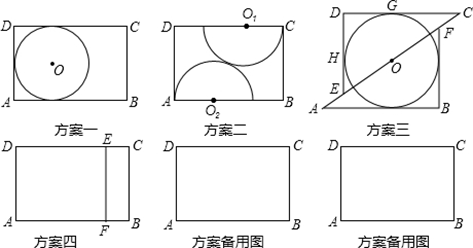
(年浙江宁波12分)课本作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多种剪法,图1是其中的一种方法:
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C= ,试画出示意图,并求出
,试画出示意图,并求出 所有可能的值;
所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.
(年山西省11分)课程学习:正方形折纸中的数学.
动手操作:如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.
数学思考:(1)求∠CB′F的度数;
(2)如图2,在图1的基础上,连接AB′,试判断∠B′AE与∠GCB′的大小关系,并说明理由;
解决问题:
(3)如图3,按以下步骤进行操作:
第一步:先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后继续对折,使AB与DC重合,折痕为MN,再把这个正方形展平,设EF和MN相交于点O;
第二步:沿直线CG折叠,使B点落在EF上,对应点为B′,再沿直线AH折叠,使D点落在EF上,对应点为D′;
第三步:设CG、AH分别与MN相交于点P、Q,连接B′P、PD′、D′Q、QB′,试判断四边形B′PD′Q的形状,并证明你的结论.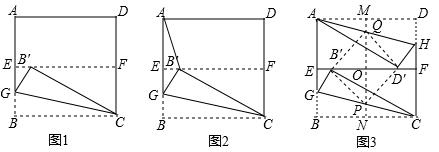
(2014年山东青岛10分)数学问题:计算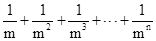 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
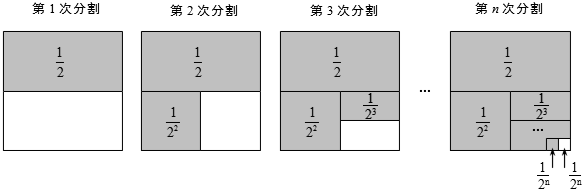
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算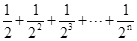 .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为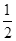 ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为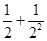 ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为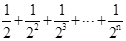 ,最后空白部分的面积是
,最后空白部分的面积是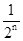 .
.
根据第n次分割图可得等式: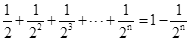 .
.
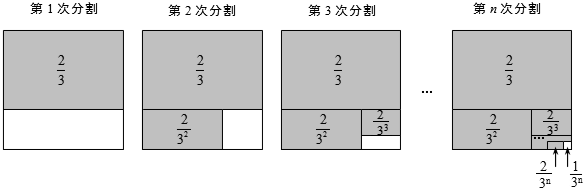
探究二:计算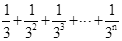 .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为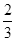 ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为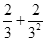 ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为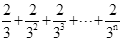 ,最后空白部分的面积是
,最后空白部分的面积是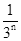 .
.
根据第n次分割图可得等式: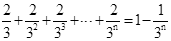 ,
,
两边同除以2,得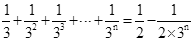 .
.
探究三:计算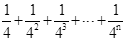 .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)
解决问题:计算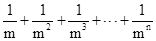 .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式: ,
所以,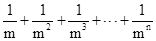 = .
= .
拓广应用:计算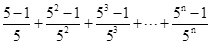 .
.