(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
(1)填空:点C的坐标是( ,),点D的坐标是( ,);
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
A1: ;A2:
;A2: ;A3:
;A3: ;
;
A4: =……An::
=……An::
(1)请观察A1,A2,A3的规律,按照规律完成填空.
(2)比较大小A1和A2
∵

∴
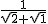
∴

(3)同理,我们可以比较出以下代数式的大小:
 ;
;
 ;
;

某开发区为改善居民住房条件,每年都新建一批住房,人均住房面积逐年增加[人均住房面积=(该区住房总面积/该区人口总数)(单位:m2/人)],该开发区2004年至2006年每年年底人均住房面积和人口总数的统计如图1,图2.
请根据图1,图2提供的信息解答下面问题:(1)该区2005年和2006年两年中哪一年比上一年增加的住房面积多?多增加多少平方米?
(2)由于经济发展需要,预计到2008年底该区人口总数比2006年底增加2万人,为使到2008年底该区人均住房面积达到11m2/人,试求2007年和2008年这两年该区住房总面积的年平均增长率为多少
如图,AB=BC,AB⊥BC于B,FC⊥BC于C,E为BC上一点,BE=FC,请探求AE与BF的关系,并说明理由.
一次统计八年级若干名学生参加歌唱比赛成绩的频数分布直方图如图,请根据这个直方图回答下面的问题:
(1)参加比赛的总人数是多少?
(2)估计这次比赛的平均成绩是多少?
(3)请把它补画成频数分布折线统计图.