（百色）抛物线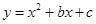
经过A（0，2），B（3，2）两点，若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动，点E的速度是每秒1个单位长度，点D的速度是每秒2个单位长度．
（1）求抛物线与x轴的交点坐标；
（2）若点C为抛物线与x轴的交点，是否存在点D，使A、B、C、D四点围成的四边形是平行四边形？若存在，求点D的坐标；若不存在，说明理由；
（3）问几秒钟时，B、D、E在同一条直线上？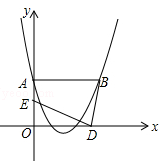
已知关于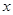
的方程
．
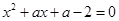（1）若该方程的一个根为1，求a的值及该方程的另一根；
（2）求证：不论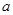
取何实数，该方程都有两个不相等的实数根．
如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD＝∠C，AB＝6，AD＝4，求线段CD的长．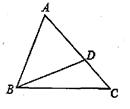
解方程：
（1）
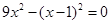
（2）
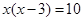
（3）
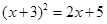
（本题14分）在同一平面直角坐标系中有6个点A（1，1），B（-3，-1），C（-3，1），D（-2，-2），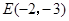
，
．
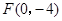（1）画出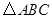
的外接圆⊙P，并指出点
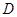与⊙P的位置关系；
（2）若将直线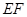
沿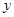
轴向上平移，当它经过点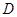时，设此时的直线为
．
①判断直线与⊙P的位置关系，并说明理由；
②再将直线绕点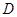按顺时针方向旋转，当它经过点
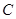时，设此时的直线为
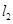．求直线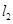与⊙P的劣弧
围成的图形的面积S（结果保留
）
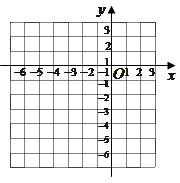
（本题12分）如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数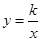
图像的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F，已知B（1，3）.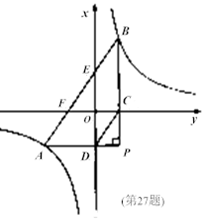
（1）k=；
（2）试说明AE=BF;
（3）当四边形ABCD的面积为
时，求点P的坐标.