(贵港)如图,抛物线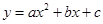 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为 .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
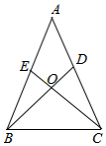
如图,已知 , , 和 相交于点 .
(1)求证: ;
(2)判断 的形状,并说明理由.
小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间 (单位:秒)与训练次数 (单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求 与 之间的函数关系式;
(2)当 的值为6,8,10时,对应的函数值分别为 , , ,比较 与 的大小: .

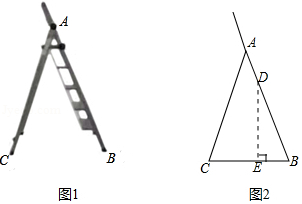
人字折叠梯完全打开后如图1所示, , 是折叠梯的两个着地点, 是折叠梯最高级踏板的固定点.图2是它的示意图, , , ,求点 离地面的高度 .(结果精确到 ;参考数据 , , ,
解方程组:
计算: .