（百色）某次知识竞赛有20道必答题，每一题答对得10分，答错或不答都扣5分，3道抢答题，每一题抢答对得10分，抢答错扣20分，抢答不到不得分也不扣分．甲乙两队决赛，甲队必答题得了170分，乙队必答题只答错了1题．
（1）甲队必答题答对答错各多少题？
（2）抢答赛中，乙队抢答对了第1题，又抢到了第2题，但还没作答时，甲队拉拉队队员小黄说：“我们甲队输了！”，小汪说：“小黄的话不一定对！”，请你举一例说明“小黄的话”有何不对．
（本题8分）如图，网络中每个小正方形的边长为1，点
的坐标为
．
（1）画出直角坐标系（要求标出
轴，
轴和原点）并写出点
的坐标；
（2）以
为基本图形，利用轴对称或旋转或平移设计一个图案，说明你的创意．
解：（1）点的坐标是；
（2）图案设计的创意是．
（本题7分） 化简求值：
x=2sin45°-1
已知抛物线
经过点A(5,0)，且满足bc=0，b<c．
(1)求该抛物线的解析式；
(2)点M在直线
上，点P在抛物线上，求当以O、A、P、M为顶点的四边形为平行四边形时的P点坐标.
在△ABC中，D为AB边上一点，过点D作DE∥BC交AC于点E，以DE为折线，将△ADE翻折，设所得的△A’DE与梯形DBCE重叠部分的面积为y
.
(1)如图(甲)，若∠C=90°，AB=10，BC=6，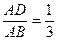
，则y的值为；
(2)如图(乙)，若AB=AC=10，BC=12，D为AB中点，则y的值为；
(3)若∠B=30°，AB=10，BC=12，设AD=x.
①求y与x的函数解析式；
②y是否有最大值，若有，求出y的最大值；若没有，请说明理由.
图(甲)图(乙)备用图
若△ABC和△ADE均为等边三角形，M、N分别是BE、CD的中点．
(1)当△ADE绕A点旋转到如图
①的位置时，求证：CD=BE，△AMN是等边三角形；
(2) 如图②，当∠EAB=30°，AB＝12，AD=
时，求AM的长．
 |
 |
||
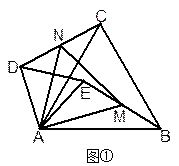