(黔西南州)如图所示,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切
(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.求弦CE的长.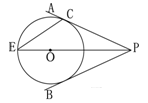
东营市“创建文明城市”活动如火如荼的展开.某中学为了搞好“创城”活动的宣传,校学生会就本校学生对东营“市情市况”的了解程度进行了一次调查测试.经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60—69分;C:70—79分;D:80—89分;E:90—100分).请你根据图中提供的信息解答以下问题: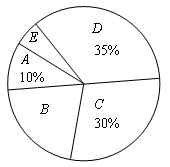
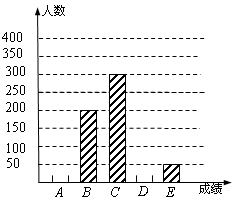
(1)求该校共有多少名学生;
(2)将条形统计图补充完整;
(3)在扇形统计图中,计算出“60—69分”部分所对应的圆心角的度数;
(4)从该校中任选一名学生,其测试成绩为“90—100分”的概率是多少?
先化简再计算: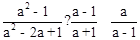 ,再选取一个你喜欢的数代入求值.
,再选取一个你喜欢的数代入求值.
已知抛物线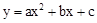 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).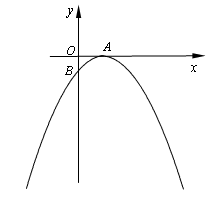
(1)求抛物线的解析式;
(2)在对称轴右侧的抛物线上找出一点C,使以BC为直径的圆经过抛物线的顶点A.并求出点C的坐标以及此时圆的圆心P点的坐标.
(3)在(2)的基础上,设直线x=t(0<t<10)与抛物线交于点N,当t为何值时,△BCN的面积最大,并求出最大值.
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=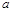 ,其中
,其中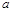 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.