（年贵州省黔南州）为了解都匀市交通拥堵情况，经统计分析，都匀彩虹桥上的车流速度v（千米/时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/时；当车流密度为20辆/千米时，车流速度为80千米/时．研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．
（1）求彩虹桥上车流密度为100辆/千米时的车流速度；
（2）在交通高峰时段，为使彩虹桥上车流速度大于40千米/时且小于60千米/时，应控制彩虹桥上的车流密度在什么范围内？
（3）当车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量=车流速度×车流密度．当20≤x≤220时，求彩虹桥上车流量y的最大值．
如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D，DE⊥DB交AB于点E，设⊙O是△BDE的外接圆．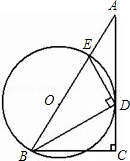
（1）求证：AC是⊙O的切线；
（2）若DE=2，BD=4，求AE的长．
先化简再求值
，已知a2+2a﹣7=0．
已知二次函数的图象经过A（2，0）、C（0，12）两点，且对称轴为直线x=4．设顶点为点P，与x轴的另一交点为点B．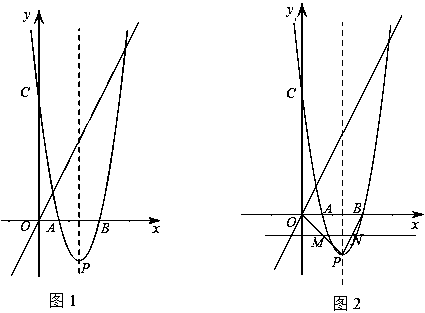
（1）求二次函数的解析式及顶点P的坐标；
（2）如图1，在直线y=2x上是否存在点D，使四边形OPBD为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；
（3）如图2，点M是线段OP上的一个动点（O、P两点除外），以每秒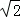
个单位长度的速度由点P向点O 运动，过点M作直线MN∥x轴，交PB于点N．将△PMN沿直线MN对折，得到△P1MN．在动点M的运动过程中，设△P1MN与梯形OMNB的重叠部分的面积为S，运动时间为t秒．求S关于t的函数关系式．
如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC，交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
（1）求证：AE与⊙O相切；
（2）其中BC=6，cosC=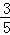
，求⊙O的半径；
（3）如果⊙O在如图位置开始沿着射线BA方向移动，当OB满足什么条件时，⊙O与直线AC相交？（直接写出结果）
某公司生产的一种时令商品每件成本为20元，经过市场调研发现，这种商品在未来20天内的日销售量m（件）与时间t（天）的关系如表：
| 时间t（天） |
1 |
3 |
6 |
10 |
… |
| 日销售量m（件） |
94 |
90 |
84 |
76 |
… |
未来20天内每天的价格y（元/件）与时间t（天）的函数关系式为y=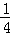
t+25（1≤t≤20且t为整数）．
（1）认真分析表中的数据，用所学过的函数知识，确定一个满足这些数据的m（件）与t（天）之间的关系式；
（2）设未来20天日销售利润为p（元）．请求出p（元）与t（天）之间的关系式；并预测未来20天中哪一天的日销售利润最大，最大日销售利润是多少？