(1)如图1,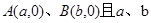 满足
满足 .
.
①求 的值;
的值;
②若C(-6,0),连CB,作BE⊥CB,垂足为B,且BC=BE,连AE交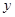 轴于P,求P点坐标.
轴于P,求P点坐标.
(2)如图2,若A(6,0),B(0,3),点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点Q运动时间为 秒,过Q点作直线AB的垂线,垂足为D,直线QD与
秒,过Q点作直线AB的垂线,垂足为D,直线QD与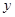 轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的
轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的 值以及相应的E点坐标.
值以及相应的E点坐标.
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上。点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
(1)当t = 2时,tan∠NAO = ;
(2)在直角坐标系中,取定点P(3,8),则在点M运动过程中,当以M、N、C、P为顶点的四边形是梯形时,点M的坐标为.
某公司新开发一种电子产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y =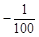 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润= 销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润= 销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳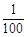 x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
(1)若在国内销售,当月销售量为1000件时,该产品的销售价格和月利润分别是多少元?当月销售量为多少件时,在国内销售的月利润最大?最大利润是多少?
(2)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(3)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如下表:
| 质量/kg |
0.5 |
0.6 |
0.7 |
1.0 |
1.2 |
1.6 |
1.9 |
| 数量/条 |
1 |
8 |
15 |
18 |
5 |
1 |
2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点).
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
如图1,小明将量角器和一块含30°角的直角三角板ABC紧靠着放在同一平面内,使直角边BC与量角器的0°线CD在同一直线上(即点B、C、O、D在同一直线上),O为量角器圆弧所在圆的圆心,∠ACB=90°,∠CAB=30°, BC=6cm.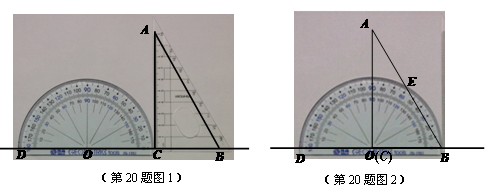
(1)判断AC是不是⊙O的切线,并说明理由.
(2)将直角三角板ABC沿CD方向平移,使点C落在点O上.此时点B落在点C原位置上(如图2),AB交⊙O于点E,则弧BE的长是多少?
如图,函数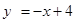 的图象与函数
的图象与函数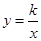 (
(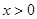 )的图象交于A(a,1)、B(1,b)两点.
)的图象交于A(a,1)、B(1,b)两点.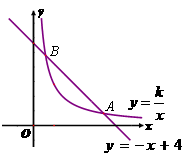
(1)求k的值;
(2)设y1=-x+4, ,利用图象分别写出x>1时y1和y2的取值范围,以及y1与y2的大小关系.
,利用图象分别写出x>1时y1和y2的取值范围,以及y1与y2的大小关系.