（本小题12分）小明有5张写着不同数字的卡片，请按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少?
答：我抽取的2张卡片是 、 ，乘积的最大值为 ．
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少?
答：我抽取的2张卡片是 、 ，商的最小值为 ．
（3）从中取出4张卡片，用学过的运算方法，使结果为24．如何抽取？写出运算式子．（写出一种即可）
答：我抽取的4张卡片是 、 、 、 ，
算24的式子为 ．
（本小题8分）如图，⊙O的直径AB垂直于弦CD，垂足为点E，过点C作⊙O 的切线，交AB的延长线于点P，联结PD．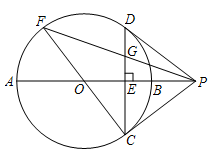
（1）判断直线PD与⊙O的位置关系，并加以证明；
（2）连接CO并延长交⊙O于点F，联结FP交CD于点G，如果CF=10，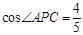
，求EG的长．
（本小题6分）如图，点C，D在线段BF上，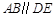
，
，
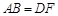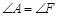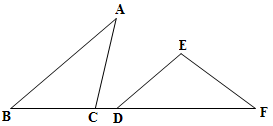
．求证：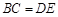
．
给出定义，若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．
（1）在你学过的特殊四边形中，写出两种勾股四边形的名称；
（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，连接AD，DC，CE，已知∠DCB=30°．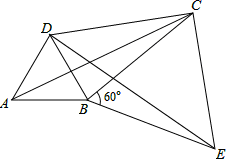
①求证：△BCE是等边三角形；
②求证：DC2+BC2=AC2，即四边形ABCD是勾股四边形．
抗震救灾重建家园，为了修建在地震中受损的一条公路，若由甲工程队单独修需3个月完成，每月耗资12万元；若由乙工程队单独修建需6个月完成，每月耗资5万元．
（1）请问甲、乙两工程队合作修建需几个月完成？共耗资多少万元？
（2）若要求最迟4个月完成修建任务，请你设计一种方案，既保证按时完成任务，又最大限度节省资金．（时间按整月计算）
为了解某校七，八年级学生的睡眠情况，随机抽取了该校七，八年级部分学生进行调查，已知抽取七年级与八年级的学生人数相同，利用抽样所得的数据绘制如下统计图表．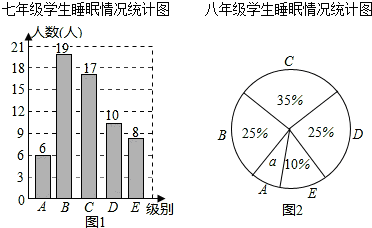
睡眠情况分组表（单位：时）
| 组别 |
睡眠时间x |
| A |
x≤7．5 |
| B |
7．5≤x≤8．5 |
| C |
8．5≤x≤9．5 |
| D |
9．5≤x≤10．5 |
| E |
x≥10．5 |
根据图表提供的信息，回答下列问题：
（1）求统计图中的a；
（2）抽取的样本中，八年级学生睡眠时间在C组的有多少人？
（3）已知该校七年级学生有755人，八年级学生有785人，如果睡眠时间x（时）满足：7．5≤x≤9．5，称睡眠时间合格，试估计该校七、八年级学生中睡眠时间合格的共有多少人？