(本小题10分)已知 、
、 为椭圆
为椭圆 的左、右焦点,过
的左、右焦点,过 做椭圆的弦
做椭圆的弦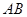 .
.
(Ⅰ)求证: 的周长是常数;
的周长是常数;
(Ⅱ)若 的周长为16,且
的周长为16,且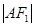 、
、 、
、 成等差数列,求椭圆方程.
成等差数列,求椭圆方程.
(本题14分)
(1)将一颗骰子(正方体形状)先后抛掷2次,得到的点数分别记为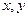 ,
,
求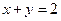 及
及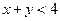 的概率;
的概率;
(2)从区间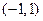 中随机取两个数
中随机取两个数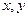 ,求
,求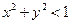 的概率.
的概率.
(本题14分) 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 |
频数 |
频率 |
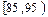 |
① |
0. 025 |
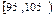 |
0.050 |
|
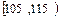 |
0.200 |
|
 |
12 |
0.300 |
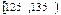 |
0.275 |
|
 |
4 |
② |
| [145,155] |
0.050 |
|
| 合计 |
③ |
|
(本小题14分)
已知函数 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数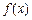 在D上的最小值,
在D上的最小值, 表示函数
表示函数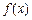 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得 对任意的
对任意的 成立,则称函数
成立,则称函数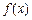 为
为 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(2)已知函数 试判断
试判断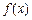 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
(本小题满分12分)
已知点F是抛物线C: 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= 。
。
(1)求点S的坐标;
(2)以S为圆心的动圆与 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
①判断直线MN的斜率是否为定值,并说明理由;
②延长NM交 轴于点E,若|EM|=
轴于点E,若|EM|= |NE|,求cos∠MSN的值。
|NE|,求cos∠MSN的值。
(本小题满分12分)已知数列 满足
满足 且
且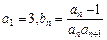 ,数列
,数列 的前
的前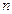 项和为
项和为 。
。
(1)求数列 的通项
的通项 ; (2)求
; (2)求 ;
;
(3)设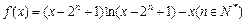 ,求证:
,求证: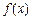 ≥
≥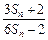 。
。