(本小题满分12分)已知椭圆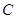 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆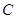 的方程;
的方程;
(2)设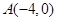 ,过点
,过点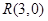 作与
作与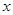 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆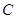 于
于 ,
,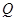 两点,连接
两点,连接 ,
, 分别交直线
分别交直线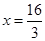 于
于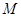 ,
, 两点,若直线
两点,若直线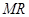 、
、 的斜率分别为
的斜率分别为 、
、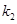 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
已知函数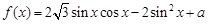 ,
,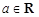 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若函数 有零点,求实数
有零点,求实数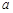 的取值范围.
的取值范围.
对于自然数数组 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 的极差
的极差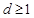 ,可实施如下操作
,可实施如下操作 :若
:若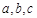 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若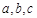 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为 ,其级差为
,其级差为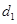 .若
.若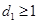 ,则继续对
,则继续对 实施操作
实施操作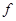 ,…,实施
,…,实施 次操作后的结果记为
次操作后的结果记为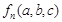 ,其极差记为
,其极差记为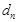 .例如:
.例如: ,
,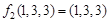 .
.
(1)若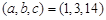 ,求
,求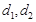 和
和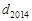 的值;
的值;
(2)已知 的极差为
的极差为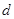 且
且 ,若
,若 时,恒有
时,恒有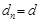 ,求
,求 的所有可能取值;
的所有可能取值;
(3)若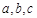 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在 满足
满足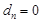 .
.
已知椭圆 的离心率为
的离心率为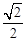 ,其短轴两端点为
,其短轴两端点为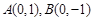 .
.
(1)求椭圆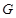 的方程;
的方程;
(2)若 是椭圆
是椭圆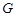 上关于
上关于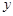 轴对称的两个不同点,直线
轴对称的两个不同点,直线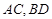 与
与 轴分别交于点
轴分别交于点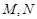 .判断以
.判断以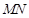 为直径的圆是否过点
为直径的圆是否过点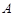 ,并说明理由.
,并说明理由.
已知函数 .
.
(1)当 时,求函数
时,求函数 值域;
值域;
(2)当 时,求函数
时,求函数 的单调区间.
的单调区间.
某单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5.该地区汽车限行规定如下:
| 车尾号 |
0和5 |
1和6 |
2和7 |
3和8 |
4和9 |
| 限行日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).