(本小题满分12分)
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e],f(x)=ax+lnx(其中e是自然对数的底数,a∈R)
(1)求f(x)的解析式;
(2)设g(x)= ,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+
,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+ ;
;
(3)是否存在实数a,使得当x∈[-e,0)时f(x)的最小值是3 如果存在,求出实数a的值;如果不存在,请说明理由.
(本小题满分12分)
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA?
已知数列 ,设
,设 ,数列
,数列 。
。
(1)求证: 是等差数列; (2)求数列
是等差数列; (2)求数列 的前n项和Sn.
的前n项和Sn.
.(本小题满分12分)
设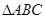 的内角
的内角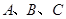 的对边分别为
的对边分别为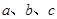 ,且
,且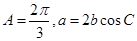 ,求:
,求:
(1)角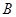 的值;
的值;
(2)函数 在区间
在区间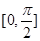 上的最大值及对应的x值.
上的最大值及对应的x值.
(本小题满分14分)已知椭圆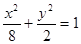 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
(1)当 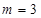 时,判断直线l与椭圆的位置关系;
时,判断直线l与椭圆的位置关系;
(2)当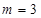 时,P为椭圆上的动点,求点P到直线l距离的最小值;
时,P为椭圆上的动点,求点P到直线l距离的最小值;
(3)如图,当l交椭圆于A、B两个不同点时,求证:
直线MA、MB与x轴始终围成一个等腰三角形