如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:
(1)若传送带静止,旅行包滑到B点时,人若没有及时取下,旅行包将从B端滑落,则包的落地点距B端的水平距离为多少?
(2)设皮带轮顺时针匀速运动,若皮带轮的角速度ω1=40rad/s,旅行包落地点距B端的水平距离又为多少?
一列简谐横波由质点A向质点B传播。已知A、B两点相距4m,这列波的波长大于2m而小于20m。上图表示在波的传播过程中A、B两质点的振动的图象。求波的传播速度。
如图所示,一块涂有炭黑玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上运动。一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得 OA=1cm,OB=4cm,OC=9cm.求外力F的大小。(g=10m/s2,不计阻力)
如图所示,将质量为 的平台A连结在劲度系数
的平台A连结在劲度系数 的弹簧上端,弹簧下端固定在地上,形成竖直方向的弹簧振子,在A的上方放置
的弹簧上端,弹簧下端固定在地上,形成竖直方向的弹簧振子,在A的上方放置 的物块B,使A、B一起上下振动,弹簧原长为5cm.A的厚度可忽略不计,
的物块B,使A、B一起上下振动,弹簧原长为5cm.A的厚度可忽略不计, 取10
取10 求:
求: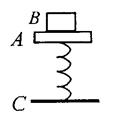
(1)当系统做小振幅简谐振动时,A的平衡位置离地面C多高?
(2)当振幅为0.5cm时,B对A的最大压力有多大?
(3)为使B在振动中始终与A接触,振幅不能超过多大?
如图所示,一等腰直角棱镜,放在真空中,AB=AC=d.在棱镜侧面AB左方有一单色光源S,从S发出的光线SD以60°入射角从AB侧面中点射入,当它从侧面AC射出时,出射光线偏离入射光线的偏向角为30°,若测得此光线传播的光从光源到棱镜面AB的时间跟在棱镜中传播的时间相等,那么点光源S到棱镜AB侧面的垂直距离是多少?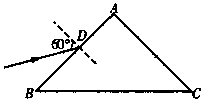
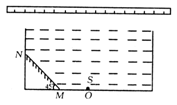
如图所示,一不透明的圆柱形容器内装满折射率n =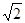 的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+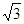 )dm,OM = 1dm,在容器中央正上方1 dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)
)dm,OM = 1dm,在容器中央正上方1 dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)