定义在（0，＋∞）上的函数f（x），对于任意的m，n∈（0，＋∞），都有f（mn）＝f（m）＋f（n）成立，当x＞1时，f（x）＜0．
（1）求证：1是函数f（x）的零点；
（2）求证：f（x）是（0，＋∞）上的减函数；
（3）当f （2）＝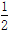 
时，解不等式f （ax＋4）＞1．
（本小题满分12分）
已知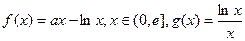
，其中
是自然常数，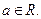
（1）讨论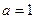
时,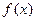 
的单调性、极值；
（2）求证：在（1）的条件下，
；
（3）是否存在实数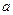
，使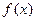的最小值是3，若存在，求出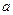的值；若不存在，说明理由.
（本小题满分12分）如图，在四棱锥E－ABCD中，AB⊥平面BCE，CD⊥平面BCE，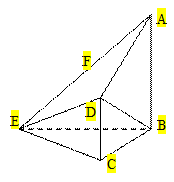
AB=BC=CE=2CD=2，∠BCE=1200，F为AE中点。
(Ⅰ) 求证：平面ADE⊥平面ABE ；
(Ⅱ)求二面角A—EB—D的大小的余弦值；
（Ⅲ）求点F到平面BDE的距离.
如右图所示，四边形ABCD内接于⊙O，AB＝AD，过A点的切线交CB的延长线于E点．
求证：AB2＝BE·CD.
如右图所示，AB是⊙O的直径，C、F为⊙O上的点，CA是∠BAF的角平分线，过点C作CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M.
(1)求证：DC是⊙O的切线；
(2)求证：AM·MB＝DF·DA.
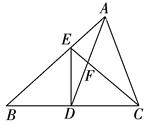如右图，已知在△ABC中，D是BC边上的中点，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F.
(1)求证：△ABC∽△FCD.
(2)若S△FCD＝5，BC＝10，求DE的长．