已知椭圆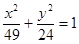 上一点
上一点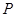 与椭圆的两个焦点
与椭圆的两个焦点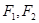 的连线互相垂直.
的连线互相垂直.
(1)求离心率和准线方程;
(2)求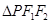 的面积.
的面积.
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数 的解析式,并写出
的解析式,并写出 的单调减区间;
的单调减区间;
(2)已知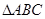 的内角分别是A,B,C,若
的内角分别是A,B,C,若 的值.
的值.
已知 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若 是增函数,求实数
是增函数,求实数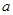 的取值范围;
的取值范围;
(2)当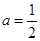 时,求函数
时,求函数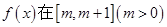 上的最小值;
上的最小值;
(3)求证: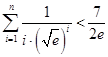 .
.
已知定点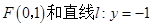 ,过点F且与直线
,过点F且与直线 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若点A的坐标为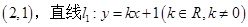 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线 于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件: .
.
(ⅰ)求 的值;
的值;
(ⅱ)求证:点 ,
, ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.
设向量
 ,定义一种向量积
,定义一种向量积 .
.
已知向量 ,
, ,点
,点 为
为 的图象上的动点,点
的图象上的动点,点
为 的图象上的动点,且满足
的图象上的动点,且满足 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.设函数
的图象.设函数

 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.