为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
| 组别 |
锻炼次数 |
频数(人) |
频率 |
| 1 |
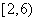 |
2 |
0.04 |
| 2 |
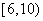 |
11 |
0.22 |
| 3 |
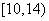 |
16 |
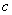 |
| 4 |
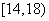 |
15 |
0.30 |
| 5 |
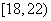 |
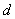 |
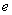 |
| 6 |
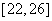 |
2 |
0.04 |
| [ |
合计 |
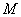 |
1.00 |
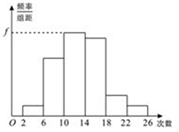
(1)求频率分布表中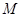 、
、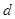 、
、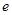 及频率分布直方图中
及频率分布直方图中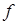 的值;
的值;
(2)求参加锻炼次数的众数(直接写出答案,不要求计算过程);
(3)若参加锻炼次数不少于18次为及格,估计这次体育锻炼的及格率。
如图,已知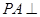 面
面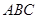 ,
,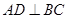 于D,
于D,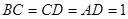 。
。
(1)令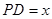 ,
,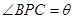 ,试把
,试把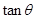 表示为
表示为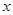 的函数,并求其最大值;
的函数,并求其最大值;
(2)在直线PA上是否存在一点Q,使得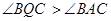 ?
?
若实数 、
、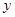 、
、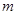 满足
满足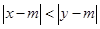 ,则称
,则称 比
比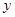 接近
接近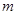 .
.
(1)若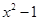 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)已知函数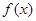 的定义域
的定义域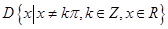 .任取
.任取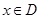 ,
,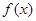 等于
等于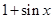 和
和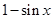 中接近0的那个值.写出函数
中接近0的那个值.写出函数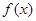 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
已知复数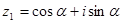 ,
, 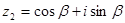 ,
, 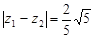 ,
,
求:(1)求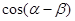 的值;(2)若
的值;(2)若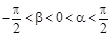 ,且
,且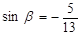 ,求
,求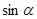 的值.
的值.
(本小题14分)已知函数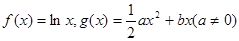
(Ⅰ)若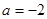 时,函数
时,函数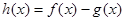 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数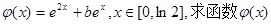 的最小值;
的最小值;
(Ⅲ)设函数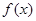 的图象C1与函数
的图象C1与函数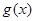 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(本小题14分)设 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数 与
与 的图象关于
的图象关于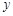 轴对称,且当
轴对称,且当 时,
时,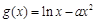 .
.
(1)求函数 的解析式;
的解析式;
(2)若对于区间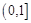 上任意的
上任意的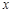 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.