已知二次函数f(x)=ax2+bx+1(a,b∈R,a>0),设方程f(x)=x的两个实数根为x1和x2.
(1)如果x1<2<x2<4,设二次函数f(x)的对称轴为x=x0,求证:x0>﹣1;
(2)如果|x1|<2,|x2﹣x1|=2,求b的取值范围.
(本小题满分12分)
甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多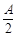 ,乙公司自1993年起逐年的市场占有率如图所示:
,乙公司自1993年起逐年的市场占有率如图所示: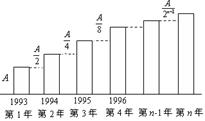
(I)求甲、乙公司第n年市场占有率的表达式;
(II)根据甲、乙两家公司所在地的市场规律,如果某公司的市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算,2012年之前,不会出现兼并局面,试问2012年是否会出现兼并局面,并说明理由.
(本小题满分12分)
如图,在平面直角坐标系中,锐角 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点.
(Ⅰ)如果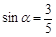 ,点
,点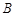 的横坐标为
的横坐标为 ,求
,求 的值;
的值;
(Ⅱ)已知点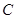
 ,求函数
,求函数 的值域.
的值域.
.(本小题满分12分)
为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为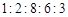 ,最后一组数据的频数是6.
,最后一组数据的频数是6.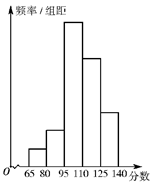
(Ⅰ)估计该校高三学生质检数学成绩在125~140分之间的概率,并求出样本容量;
(Ⅱ)从样本中成绩在65~95分之间的学生中任选两人,求至少有一人成绩在65~80分之间的概率.
已知定义在R上的函数 ,其中a、b为常数。
,其中a、b为常数。
(1)若曲线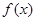 在点
在点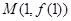 处的切线方程为
处的切线方程为 ,求a、b的值;
,求a、b的值;
(2)若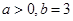 ,且函数
,且函数 在
在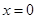 处取得最大值,求实数a的取值范围。
处取得最大值,求实数a的取值范围。
已知椭圆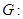
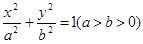 的离心率为
的离心率为 =
= ,椭圆
,椭圆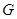 上的点
上的点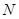 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆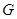 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点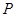 在椭圆上,且位于
在椭圆上,且位于 轴的上方,
轴的上方, .
.
(I)求椭圆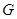 的方程;
的方程;
(II)求点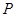 的坐标;
的坐标;
(III)设 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点, 到直线AP的距离等于
到直线AP的距离等于 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离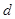 的最小值.
的最小值.