一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N*)件.当x≤20时,年销售总收入为(33x-x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,
(1)y(万元)与x(件)的函数关系式为?
(2)该工厂的年产量为多少件时,所得年利润最大,并求出最大值.(年利润=年销售总收入-年总投资)
对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.
| 观测次数i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 观测数据ai |
40 |
41 |
43 |
43 |
44 |
46 |
47 |
48 |
在上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中是这8个数据的平均数),求输出的S的值.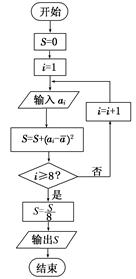
.(本小题满分14分)
设函数 .
.
若 ,求
,求 的最小值;
的最小值;
若当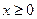 时
时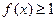 ,求实数
,求实数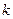 的取值范围.
的取值范围.
.(本小题共13分)
已知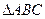 的边
的边 所在直线的方程为
所在直线的方程为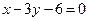 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
.
(1)求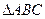 外接圆的方程;
外接圆的方程;
(2)一动圆过点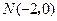 ,且与
,且与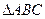 的
的
外接圆外切,求此动圆圆心的轨迹方程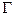 ;
;
(3)过点 斜率为
斜率为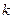 的直线与曲线
的直线与曲线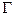 交于相异的
交于相异的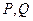 两点,满足
两点,满足 ,求
,求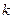 的取值范围.
的取值范围.
..(本小题满分12分)
数列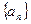 的各项均为正数,
的各项均为正数,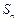 为其前
为其前 项和,对于任意
项和,对于任意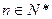 ,总有
,总有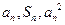 成等差数列.
成等差数列.
(1)求数列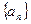 的通项公式;
的通项公式;
(2)设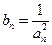 ,数列
,数列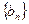 的前
的前 项和为
项和为 ,求证:
,求证: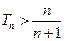 .
.
.
如图,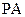 垂直于矩形
垂直于矩形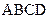 所在的平面,
所在的平面,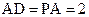 ,
,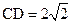 ,
, 、
、 分别是
分别是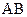 、
、 的中点.
的中点.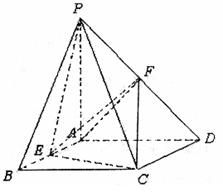
(1)求证: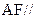 平面
平面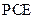 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求四面体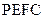 的体积
的体积