已知数列{an}的前三项与数列{bn}的前三项相同，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意n∈N*都成立，数列{bn＋1－bn}是等差数列．
（1）求数列{an}与{bn}的通项公式；
（2）是否存在k∈N*，使得（bk－ak）∈（0,1）？请说明理由．
（本小题满分12分）在三角形ABC中，∠A，∠B，∠C的对边分别为
且
（1）求∠A；
（2）若
，求
的取值范围.
（本小题满分12分）函数
在一个周期内的图象如图所示，
为图象的最高点，
、
为图象与
轴的交点，且
为正三角形.
（1）求
的值及函数
的值域；
（2）若
，且
，求
的值.
（本小题满分12分）已知p：函数
在
上单调递增；q：关于
的不等式
的解集为R．若
为真命题，
为假命题，求
的取值范围．
（本小题满分10分）选修4
4：坐标系与参数方程
在极坐标系内，已知曲线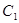
的方程为
，以极点为原点，极轴方向为
正半轴方向，利用相同单位长度建立平面直角坐标系，曲线
的参数方程为
（
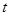为参数）.
（1）求曲线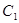的直角坐标方程以及曲线
的普通方程；
（2）设点
为曲线上的动点，过点作曲线
的切线，求这条切线长的最小值.
（本小题满分10分）选修4
1：几何证明选讲
如图，C是以AB为直径的半圆O上的一点，过C的直线交直线AB于E，交过A点的切线于D，BC∥OD .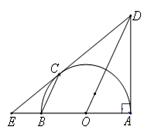
（1）求证：DE是圆O的切线；
（2）如果AD ="AB" = 2，求EB的长.