行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
先化简,再求值:其中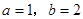
(1) ;(2)
;(2)
计算:
(1)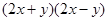 (2)
(2)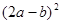
(3) (4)4-
(4)4- -(2-
-(2- )+
)+
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.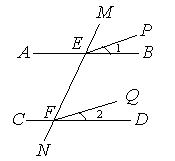
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.
解:∵EF∥AD,
∴∠2=()
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥()
∴∠BAC+=180 o()
∵∠BAC=70 o,
∴∠AGD=。
如图, 与
与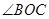 是邻补角,OD、OE分别是
是邻补角,OD、OE分别是 与
与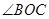 的平分线,试判断OD与OE的位置关系,并说明理由.
的平分线,试判断OD与OE的位置关系,并说明理由.
先化简,再求值: ,其中a=-2。
,其中a=-2。