已知:已知函数y = y1 +y2,y1与x成正比例,y2与x成反比例,且当x = 1时,y =-1;当x = 3时,y = 5.求y关于x的函数关系式.
袋中装有除数字不同其它都相同的六个小球,球上分别标有数字1,2,3,4,5,6.
(1)从袋中摸出一个小球,求小球上数字小于3的概率;
(2)将标有1,2,3数字的小球取出放入另外一个袋中,分别从两袋中各摸出一个小球,
求数字之和为偶数的概率.(要求用列表法或画树状图求解)
如图,在直角坐标系中,点D在y轴上,四边形ABCD是等腰梯形,AB∥CD。已知, DO⊥AB, OE⊥BC,E、O分别为垂足,BC="BO" ,O为坐标原点。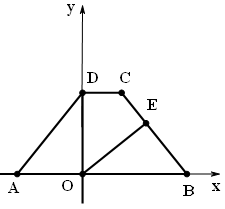
(1) 求证:DO=EO
(2) 已知:C点坐标为(4 , 8),
①求等腰梯形ABCD的腰长;
②问题探究:在这个坐标平面内是否存在点F,使以点F、D、O、E为顶点的四边形是菱形?若存在,请求出所有符合要求的F点的坐标,并说明理由;若不存在,请说明理由。
如图,在□ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为25,AB=12,求对角线AC与BD的和.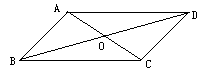
自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?