己知函数f（x）lnxaxl，其中a∈R．（1）求f（x）的-优题课

题文

己知函数f（x）=lnx-ax+l，其中a∈R．
（1）求f（x）的单调区间；
（2）当a=1时，斜率为k的直线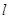与函数f（x）的图像交于两点A（x₁，y₁），B（x₂，y₂），其中x₁＜x₂，证明：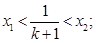
（3）是否存在k∈Z，使得f（x）+ax-2＞k（1一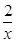）对任意x＞l恒成立？若存在，请求出k的最大值；若不存在，请说明理由．

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

已知椭圆 $C : x^{2} + 2 y^{2} = 4$ .
（1）求椭圆 $C$ 的离心率；
（2）设 $O$ 为原点，若点 $A$ 在椭圆 $C$ 上，点 $B$ 在直线 $y = 2$ 上，且 $O A ⊥ O B$ ，试判断直线 $A B$ 与圆 $x^{2} + y^{2} = 2$ 的位置关系，并证明你的结论.

已知函数 $f (x) = x \cos x - \sin x, x \in [0, \frac{π}{2}]$ .
（1）求证： $f (x) \leq 0$ ；
（2）若 $a < \frac{\sin x}{x} < b$ 对 $x \in (0, \frac{π}{2})$ 恒成立，求 $a$ 的最大值与 $b$ 的最小值.

如图，正方体 $M A D E$ 的边长为2, $B, C$ 分别为 $A M, M D$ 的中点,在五棱锥 $P - A B C D E$ 中, $F$ 为棱 $P E$ 的中点,平面 $A B F$ 与棱 $F D$ , $P C$ 分别交于 $G$ , $H$ .

（1）求证： $A B ∥ F G$ ；
（2）若 $P A ⊥$ 底面 $A B C D E$ ，且 $P A = A E$ ，求直线 $B C$ 与平面 $A B F$ 所成角的大小，并求线段 $P H$ 的长.

李明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）：

场次	投篮次数	命中次数	场次	投篮次数	命中次数
主场1	22	12	客场1	18	8
主场2	15	12	客场2	13	12
主场3	12	8	客场3	21	7
主场4	23	8	客场4	18	15
主场5	24	20	客场5	25	12

（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；
（2）从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；
（3）记为表中10个命中次数的平均数，从上述比赛中随机选择一场，记为李明在这场比赛中的命中次数，比较与的大小（只需写出结论）

如图，在 $∆ A B C$ 中， $∠ B = \frac{π}{3}, A B = 8$ ，点 $D$ 在 $B C$ 边上，且 $C D = 2$ ， $\cos ∠ A B C = \frac{1}{7}$ .
（1）求 $\sin ∠ B A D$ ；
（2）求 $B D$ ， $A C$ 的长.

试卷网试题网古诗词网作文网范文网