如图,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)若经过B、E、C三点的抛物线的解析式为y=-x2+(2b-1)x+c-5,则b=,c=(直接填空)
(2)①以P、D、E为顶点的三角形是直角三角形,则点P的坐标为(直接填空)
②若抛物线顶点为N,又PE+PN的值最小时,求相应点P的坐标.
(3)连结QN,探究四边形PMNQ的形状:
①能否成为平行四边形
②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.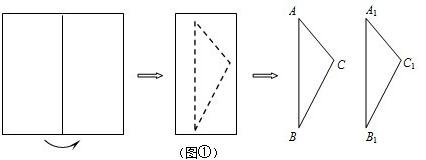
(1)将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.
①求证:四边形C1B1AB为梯形.
②若∠A="45°," ∠ABC="30°," 求∠B1C1C的度数
(2)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(3)在(2)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)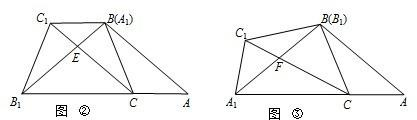
某经销商代理销售一种手机,按协议,每卖出一部手机需另交品牌代理费100元,已知该种手机每部进价800元,销售单价为1200元时,每月能卖出100部,市场调查发现,若每部手机每让利50元,则每月可多售出40部.
(1)若每月要获取36000元利润,求让利价
(利润=销售收入-进货成本-品牌代理费)
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
如图,已知AB为⊙O的直径,E是AB延长线上一点,点C是⊙O上的一点,连结EC、BC、AC,且∠BCE=∠BAC.
(1)求证:EC是⊙O的切线.
(2)过点A作AD垂直于直线EC于D,若AD=3,DE=4,求⊙O的半径.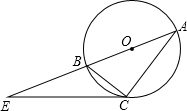
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
(1)求上述一次函数与反比例函数的表达式;
(2)设点Q是一次函数y=kx+3图象上的一点,且满足△DOQ的面积是△COD面积的2倍,直接写出点Q的坐标.
(3)若反比例函数 的图象与△ABP总有公共点,直接写出n的取值范围.
的图象与△ABP总有公共点,直接写出n的取值范围.