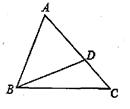
如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
（1）求证：DP是⊙O的切线；
（2）若⊙O的半径为3cm，求图中阴影部分的面积．
已知关于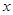
的一元二次方程
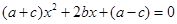，其中
、
、
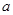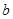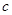分别为△ABC三边的长．
（1）如果
是方程的根，试判断△ABC的形状，并说明理由：
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点．
（1）求证：AC2＝AB·AD；
（2）求证：CE∥AD；
（3）若AD＝4， AB＝6，求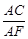
的值．
如图，已知二次函数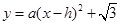
的图象经过原点0（0，0），A（2，0）．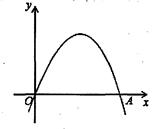
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA'，试判断点A'是否在该函数图象上？
已知关于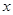
的方程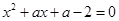
．
（1）若该方程的一个根为1，求a的值及该方程的另一根；
（2）求证：不论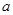
取何实数，该方程都有两个不相等的实数根．
如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD＝∠C，AB＝6，AD＝4，求线段CD的长．