某蔬菜公司收购到某种蔬菜104  吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
如图,矩形ABCD的对角线相交于点O,DE//AC,CE//DB,CE、DE交于点E,请问:四边形DOCE是什么四边形?请说明理由。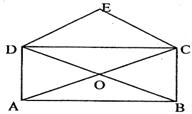
为了拉动内需,全国各地汽车购置税补贴活动在2009年正式开始.某经销商在政策出台前一个月共售出某品牌汽车的手动型和自动型共960台,政策出台后的第一个月售出这两种型号的汽车共 1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台?
(2)若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,问政策出台后的第一个月,政府对这l228台汽车用户共补贴了多少万元?
如图,在平面直角坐标系中,A(—1, 5),B(—1,0),C(—4,3)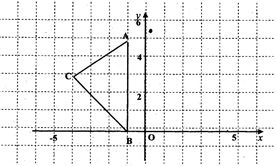
(1)求出 ABC的面积;
ABC的面积;
(2)在图中作出 ABC关于y轴的对称图形
ABC关于y轴的对称图形 A
A B
B C
C
(3)写山点A ,B
,B ,C
,C 的坐标。
的坐标。
已知点(1,3)在函数y= (x > 0)的图象
(x > 0)的图象 上,矩形ABCD的边BC在x轴上,E是对角线BD中点,函数y =
上,矩形ABCD的边BC在x轴上,E是对角线BD中点,函数y =
 (x > 0)的图象又经过A, E两点,点E的横坐标为m..解答下列问题:
(x > 0)的图象又经过A, E两点,点E的横坐标为m..解答下列问题: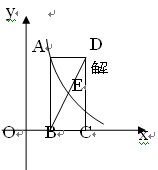
(1)求反比例函数的解析式;
(2)求点C的坐标(用m表示);
(3)当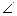 ABD=45°, 求 m
ABD=45°, 求 m 的值
的值