如图，在5×5的方格（每小格边长为1）内有4只甲虫A、B、C、D，它们爬行规律总是先左右，再上下．规定：向右与向上为正，向左与向下为负．从A到B的爬行路线记为：A→B（＋1，＋4），从B到A的爬行路线为：B→A（－1，－4），其中第一个数表示左右爬行信息，第二个数表示上下爬行信息，那么图中
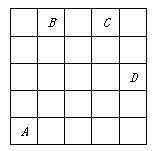
（1） A→C（ ， ），B→D（ ， ），C→ （＋1， ）；
（2） 若甲虫A的爬行路线为A→B→C→D，请计算甲虫A爬行的路程；
（3） 若甲虫A的爬行路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），（－1，－2），最终到达甲虫P处，请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置．
问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为
．
探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数
的图象性质．
①填写下表，画出函数的图象：
| x |
… |
 |
 |
 |
1 |
2 |
3 |
4 |
… |
| y |
… |
… |
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数
(x＞0)的最小值．
解决问题
⑵用上述方法解决“问题情境”中的问题，直接写出答案．
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
（1）求函数y＝
x＋3的坐标三角形的三条边长；
（2）若函数y＝x＋b（b为常数）的坐标三角形周长为16,求此三角形面积.
（本题满分10分为迎接建党90周年，某校组织了以“党在我心中”为主题的电子小报制作比赛，评分结果只有60，70，80，90，100五种．现从中随机抽取部分作品，对其份数及成绩进行整理，制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：
（1）求本次抽取了多少份作品，并补全两幅统计图；
（2）已知该校收到参赛作品共900份，请估计该校学生比赛成绩达到90分以上（含90分）的作品有多少份？
2012年5月20日是第23个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．
(1)求这份快餐中所含脂肪质量；
(2)若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．
先化简，再求值，
÷
其中x=1.