高一某班共有学生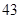 人,据统计原来每人每年用于购买饮料的平均支出是
人,据统计原来每人每年用于购买饮料的平均支出是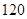 元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用
元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用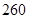 元,其中,纯净水的销售价
元,其中,纯净水的销售价 (元
(元 桶)与年购买总量
桶)与年购买总量 (桶)之间满足如图直线所示关系.
(桶)之间满足如图直线所示关系.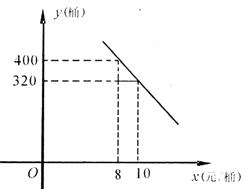
(1)求 关于
关于 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)若该班每年需要纯净水 桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.
桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.
(本小题满分12分)已知函数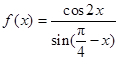 .
.
(Ⅰ)化简函数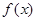 的解析式,并求其定义域和单调区间;
的解析式,并求其定义域和单调区间;
(Ⅱ)若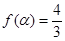 ,求
,求 的值.
的值.
设函数 ,其中
,其中 。
。
(1)当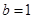 时,
时,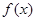 在
在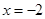 时取得极值,求
时取得极值,求 ;
;
(2)当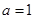 时,若
时,若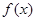 在
在 上单调递增,求
上单调递增,求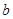 的取值范围;
的取值范围;
(3)证明对任意的正整数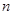 ,不等式
,不等式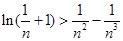 都成立。
都成立。
已知椭圆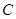 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆的短轴端点和焦点所组成的四边形周长等于8。
,椭圆的短轴端点和焦点所组成的四边形周长等于8。
(Ⅰ)求椭圆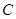 的方程;
的方程;
(Ⅱ)若过点 的直线
的直线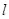 与椭圆
与椭圆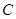 相交于
相交于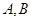 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以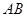 为直径的圆过椭圆
为直径的圆过椭圆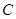 的右顶点,求直线
的右顶点,求直线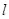 的方程。
的方程。
已知数列 满足:
满足: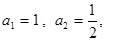 且
且 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值及数列
的值及数列 的通项公式;
的通项公式;
(Ⅱ)设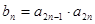 ,求数列
,求数列 的前
的前 项和
项和 ;
;
已知斜三棱柱 ,
, ,
,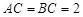 ,
, 在底面
在底面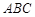 上的射影恰为
上的射影恰为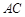 的中点
的中点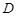 ,又知
,又知 .
.
(Ⅰ)求证: 平面
平面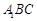 ;
;
(Ⅱ)求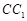 到平面
到平面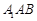 的距离;
的距离;
(Ⅲ)求二面角 的大小。
的大小。