设函数f(x)对任意x,y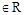 ,都有
,都有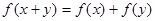 ,且
,且 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数;
(2)试问在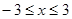 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
已知函数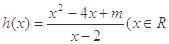 ,且
,且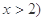 ,函数
,函数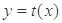 的图象经过点
的图象经过点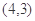 ,且
,且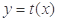 与
与 的图象关于直线
的图象关于直线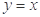 对称,将函数
对称,将函数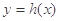 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数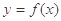 的图象.
的图象.
(Ⅰ)求函数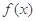 的解析式;
的解析式;
(Ⅱ)若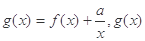 在区间
在区间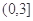 上的值不小于8,求实数
上的值不小于8,求实数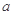 的取值范围.
的取值范围.
(III)若函数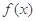 满足:对任意的
满足:对任意的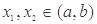 (其中
(其中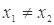 ),有
),有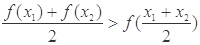 ,称函数
,称函数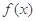 在
在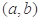 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数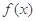 图象在
图象在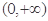 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
如图,某观测站在港口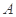 的南偏西
的南偏西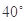 方向的
方向的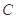 处,测得一船在距观测站
处,测得一船在距观测站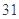 海里的
海里的 处,正沿着从港口出发的一条南偏东
处,正沿着从港口出发的一条南偏东 的航线上向港口
的航线上向港口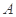 开去,当船走了
开去,当船走了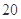 海里到达
海里到达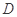 处,此时观测站又测得
处,此时观测站又测得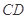 等于
等于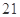 海里,问此时船离港口
海里,问此时船离港口 处还有多远?
处还有多远?
、
已知函数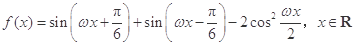 (其中
(其中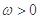 ).
).
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)若函数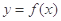 的图象与直线
的图象与直线 的两个相邻交点间的距离为
的两个相邻交点间的距离为 ,求函数
,求函数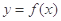 的单调增区间.
的单调增区间.
求经过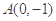 和直线
和直线 相切,且圆心在直线
相切,且圆心在直线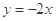 上的圆的方程.
上的圆的方程.
已知函数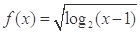 的定义域为A,函数
的定义域为A,函数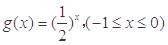 的值域为B.
的值域为B.
(Ⅰ)求 ;
;
(Ⅱ)若 ,且
,且 ,求实数
,求实数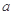 的取值范围.
的取值范围.