已知函数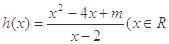 ,且
,且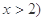 ,函数
,函数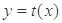 的图象经过点
的图象经过点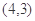 ,且
,且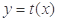 与
与 的图象关于直线
的图象关于直线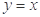 对称,将函数
对称,将函数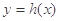 的图象向左平移2个单位后得到函数
的图象向左平移2个单位后得到函数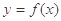 的图象.
的图象.
(Ⅰ)求函数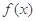 的解析式;
的解析式;
(Ⅱ)若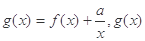 在区间
在区间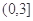 上的值不小于8,求实数
上的值不小于8,求实数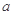 的取值范围.
的取值范围.
(III)若函数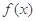 满足:对任意的
满足:对任意的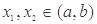 (其中
(其中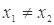 ),有
),有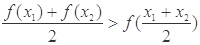 ,称函数
,称函数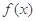 在
在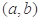 的图象是“下凸的”.判断此题中的函数
的图象是“下凸的”.判断此题中的函数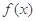 图象在
图象在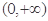 是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
是否是“下凸的”?如果是,给出证明;如果不是,说明理由.
如图, 内接于圆
内接于圆 ,
, 平分
平分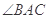 交圆
交圆 于点
于点 ,过点
,过点 作圆
作圆 的切线交直线
的切线交直线 于点
于点 .求证:
.求证: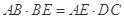 .
.
已知函数 ,
, ,直线
,直线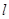 与曲线
与曲线 切于点
切于点 且与曲线
且与曲线 切于点
切于点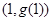 .
.
(1)求a,b的值和直线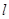 的方程;
的方程;
(2)证明: .
.
已知数列 满足
满足 ,
,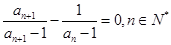 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)设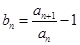 ,数列
,数列 的前
的前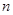 项之和为
项之和为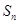 ,求
,求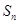 的最小值.
的最小值.
已知直线 ,一个圆的圆心
,一个圆的圆心 在
在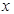 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线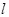 和
和 轴均相切.
轴均相切.
(1)求该圆的方程;
(2)直线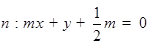 与圆
与圆 交于
交于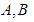 两点,且
两点,且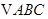 是等边三角形,求
是等边三角形,求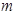 的值.
的值.
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形 和
和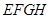 构成的面积为
构成的面积为 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形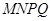 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为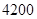 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为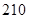 元/m2,再在四个空角(如
元/m2,再在四个空角(如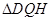 等)上铺草坪,造价为
等)上铺草坪,造价为 元/m2.设总造价为
元/m2.设总造价为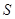 元,
元,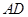 长为
长为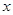 m.
m.
(1)试建立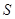 与
与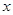 的函数关系
的函数关系
(2)当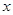 为何值时,
为何值时, 最小?并求这个最小值
最小?并求这个最小值